7. 微分

課程筆記

積分 (Integration)

單步法 (Single-Step Methods)

• 使用一步資料，推估下一步之結果。
  • 優點：單步法之步長可以彈性調整。

尤拉差分法 (Euler Difference Method)

• 原理：

  1. 若考慮 作為泰勒展開的基準點。等間距 時：。
  2. 則：
  3. 整理 可得 (尤拉前推差分法 (Euler Forward Difference Method))：
     • 註：逐步求解（顯性方法），可能會發散。
  4. 整理 可得 (尤拉後推差分法 (Euler Backward Difference Method))：
     • 註：此法需同步求解（隱性方法），但絕對收斂。
  5. 整理 可得 (中央差分法 (Central Difference Method))：
     • 註：此法為最佳方法，但需注意 的選擇。
  6. 整理 可得：
  7. 整理 可得：
  8. 整理 可得：
  9. 依此類推，可得更高階導數的數值方法。

• 泰勒級數法(數學方法，非數值方法) (Taglor Series Method)：

  • 用法：假設：
    • 則解析解：
    • 泰勒級數法：
      1. 展開：
      2. 分解：
         3. 依此類推。
      3. 代回：

• 方法：尤拉前推差分法 (Euler Forward Difference Method)：

• 方法：尤拉修正法 (Modified Euler Method)：

  • 方法：
    1. 將原本尤拉前推法的結果作為臨時解 ()：
    2. 修正後得新解：

Runge-Kutta Method

• 優點：
  • 通用的方法，適用於各種情況。
  • 較少的計算過程即可得到較高的準確度。
  • 屬於單步法（使用 即可計算 ），因此可以不等間距計算。
• 缺點：
  • 無法得到準確的誤差估計值（沒有誤差估算公式）。通常，以 再度計算，最終再與 計算結果比較，以估算其誤差量。若其差異在容許範圍內，則可接受。否則，繼續以 計算，直至其差異在容許範圍內，依此類推。
    • 為解決此問題，有延伸方法被發展。如下 Runge-Kutta-Merson Method、Runge-Kutta-Fehlberg Method。
• 原理：
  • 通式：
    • 為權重：
    • ；； 為係數
• 常用的方法：

  • 一階（就是尤拉前推差分法）：

  • 二階 (2nd order Runge-Kutta Method)（）：

    • 常用方法：
    • 原理：較為複雜，參閱註 1。

  • 三階 (3rd order Runge-Kutta Method)（）：

    • 常用方法：
    • 原理：較為複雜，參閱註 2。

  • 四階 (4th order Runge-Kutta Method)（）：

    • 常用方法：

延伸方法 - Runge-Kutta-Merson Method：

• 方法（）：

延伸方法- Runge-Kutta-Fehlberg Method：

• 常用的方法
• 方法（）：
• ★方法（）：

Example

，，，求 。

Solution-Euler Forward Difference Method

0.00	1.00	1.00	0.02	1.02
0.02	1.02	1.04	0.0208	1.0408
0.04	1.0408	1.0808	0.0216	1.0624
0.06	1.0624	1.1224	0.0224	1.0848
0.08	1.0848	1.1648	0.0233	1.1081
0.10	1.1081

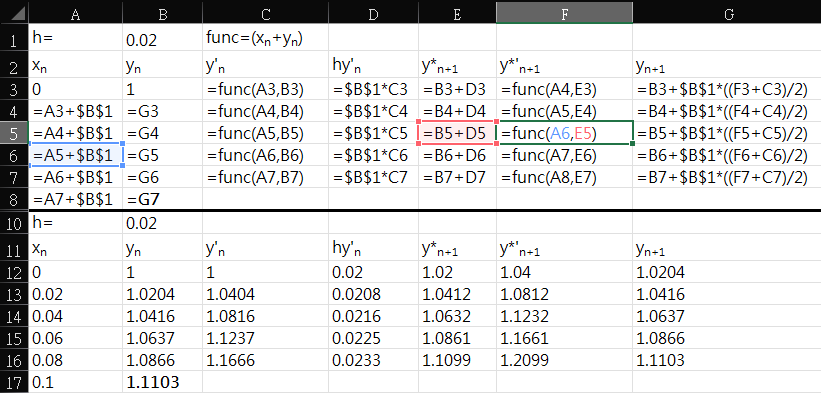
Solution-Modified Euler Method

0.00	1.00	1.00	0.02	1.02	1.04	1.0204
0.02	1.0204	1.0404	0.0208	1.0412	1.0812	1.0416
0.04	1.0416	1.0816	0.0216	1.0632	1.1232	1.0636
0.06	1.0636	1.1236	0.0225	1.0861	1.1661	1.0865
0.08	1.0865	1.1665	0.0233	1.1098	1.2098	1.1103
0.10	1.1103

Solution-2nd Order Runge-Kutta Method

1. 使用：
2. = = + =
3. = + + = + + + =
4. = + + = + =

Solution-3rd Order Runge-Kutta Method

1. 使用：
2. = +
3. = + + = + + +
4. = + + = + + =
5. = + + = + + + =

Solution-4th Order Runge-Kutta Method

1. 使用：
2. = =
3. = + + = + + =
4. = + + = + +
5. = + + = + + =
6. = + + + + = + + + =

多步法 (Multi-Step Methods)

• 以過去幾步的已知資料，推估下一步之結果。

亞當斯法 (Adams Method)

• 方法（4th order Adams Method, ）：
• 方法（5th order Adams Method, ）：
  • + + +
• 原理：較為複雜，參閱註 3。

Adams-Moulton Method

• 方法：
  • 此時，真值介於 與 之間：
    • 若 在 之間，則 與 之間的誤差為：
      
    • 如果把 Error 再加回修正值，即可得到更準的結果。

Example

，，，使用 求 。

Solution-Adams Method

0.00	-1.00	-1.00	1.00
0.20	-0.8561921	-0.8561923	0.4561921
0.40	-0.8109599	-0.8109601	0.0109599

2. 使用： + - + +
3. = + - + = + - + = + - + = + =

Solution-Adams-Moulton Method

0.00	-1.00	-1.00	1.00
0.10	x	x	x
0.20	x	x	x
0.30	x	x	x
0.40(Adams)	-0.8109687
0.40(修正)	-0.8109652
0.50(Adams)	-0.8195978
0.50(修正)	-0.8195905

2. Error(修正)= =
3. 最終，修正值加上誤差值： =

備註

註 1 - 二階 Runge-Kutta Method 原理

• 展開通式：

• 經 Taylor expansion 後，得：

• 僅三個方程式，但有四個未知數，無限多組解。故通常進考慮部分重要的結論：

  • 令 ，則 ，，
    • 得：
  • 令 ，則 ，，
    • 得：
  • 令 ，則 ，，
    • 得：
  • 令 ，則 ，，
    • 得：

註 2 - 三階 Runge-Kutta Method 原理

• 展開通式：

• 經 Taylor expansion 後，得：

• 無限多組解。故通常進考慮部分重要的結論：

  • 令 ，，則 ，，，，，
    • 得：
  • 令 ，，則 ，，，，，
    • 得：
  • 令 ，，則 ，，，，，
    • 得：

註 3 - 亞當斯法 (Adams Method) 原理

1. 當有一微分方程：。因此，。
2. 。
3. 以 Newton-Gregory 後推多項式逼近 。
   • …

Homework

題目

，，，求 。。 使用：

1. 尤拉前推差分法(Euler Forward Difference Method)
2. Modified Euler Method
3. Runge-Kutta 2nd-Order Method
4. Runge-Kutta 3rd-Order Method
5. Runge-Kutta 4th-Order Method
6. Runge-Kutta-Fehlberg 5th-Order Method

Code

針對本作業撰寫 Golang 代碼如下所示。
本作業撰寫代碼如 Golang code 1。其中包含 main()、calcEuler()、calcModifiedEuler()、calcRungeKutta2()、calcRungeKutta3()、calcRungeKutta4()、calcRungeKuttaFehlberg() 七個方法，main() 方法定義了函式 (1) 與其初始值，並用於呼叫其他方法。在最後，本作業則透過計算 Runge-Kutta-Fehlberg 5th-Order Method 以 h = 0.01 作為相對精參考值用於誤差評估。 而 calcEuler()、calcModifiedEuler()、calcRungeKutta2()、calcRungeKutta3()、calcRungeKutta4()、calcRungeKuttaFehlberg() 分別為 Modified Euler Method、Runge-Kutta 2nd-Order~4th-Order Method、Runge-Kutta-Fehlberg 5th-Order Method 的實現。透過迴圈方式由 t = 0 跌代計算到 t = 2。

package main
import (
    "fmt"
)
 
func calcEuler(f func(t, y float64) float64, t, y, h, target float64) {
    fmt.Println("----------------------------------------")
    fmt.Printf("Euler Forward Difference Method: h = %v; y(1) = %v; target = y(%v)\n", h, y, target)
    for t < target {
        y += h * f(t, y)
        t += h}
    fmt.Printf("Ans: y(%v) = %v\n", target, y)
}
 
func calcModifiedEuler(f func(t, y float64) float64, t, y, h, target float64) {
    fmt.Println("----------------------------------------")
    fmt.Printf("Modified Euler Method: h = %v; y(1) = %v; target = y(%v)\n", h, y, target)
    for t < target {
        y += h / 2 * (f(t, y) + f(t+h, y+h*f(t, y)))
        t += h}
    fmt.Printf("Ans: y(%v) = %v\n", target, y)
}
 
func calcRungeKutta2(f func(t, y float64) float64, t, y, h, target float64) {
    fmt.Println("----------------------------------------")
    fmt.Printf("Runge-Kutta 2th Order Method: h = %v; y(1) = %v; target = y(%v)\n", h, y, target)
    for t < target {
        k1 := h * f(t, y)
        k2 := h * f(t+h/2, y+k1/2)
        y += 0.5 * (k1 + k2)
        t += h}
    fmt.Printf("Ans: y(%v) = %v\n", target, y)
}
 
func calcRungeKutta3(f func(t, y float64) float64, t, y, h, target float64) {
    fmt.Println("----------------------------------------")
    fmt.Printf("Runge-Kutta 3th Order Method: h = %v; y(1) = %v; target = y(%v)\n", h, y, target)
    for t < target {
        k1 := h * f(t, y)
        k2 := h * f(t+h/2, y+k1/2)
        k3 := h * f(t+h, y-k1+2*k2)
        y += (k1 + 4*k2 + k3) / 6.0
        t += h}
    fmt.Printf("Ans: y(%v) = %v\n", target, y)
}
 
func calcRungeKutta4(f func(t, y float64) float64, t, y, h, target float64) {
    fmt.Println("----------------------------------------")
    fmt.Printf("Runge-Kutta 4th Order Method: h = %v; y(1) = %v; target = y(%v)\n", h, y, target)
    for t < target {
        k1 := h * f(t, y)
        k2 := h * f(t+h/2, y+k1/2)
        k3 := h * f(t+h/2, y+k2/2)
        k4 := h * f(t+h, y+k3)
        y += (k1 + 2*k2 + 2*k3 + k4) / 6.0
        t += h}
    fmt.Printf("Ans: y(%v) = %v\n", target, y)
}
 
func calcRungeKuttaFehlberg(f func(t, y float64) float64, t, y, h, target float64) {
    fmt.Println("----------------------------------------")
    fmt.Printf("Runge-Kutta-Fehlberg 5th Order Method: h = %v; y(1) = %v; target = y(%v)\n", h, y, target)
    err := 1e-6
    for t < target {
        k1 := h * f(t, y)
        k2 := h * f(t+h/4, y+k1/4)
        k3 := h * f(t+3*h/8, y+3*k1/32+9*k2/32)
        k4 := h * f(t+12*h/13, y+1932*k1/2197-7200*k2/2197+7296*k3/2197)
        k5 := h * f(t+h, y+439*k1/216-8*k2+3680*k3/513-845*k4/4104)
        k6 := h * f(t+h/2, y-8*k1/27+2*k2-3544*k3/2565+1859*k4/4104-11*k5/40)
        y += 16*k1/135 + 6656*k3/12825 + 28561*k4/56430 - 9*k5/50 + 2*k6/55
        err = k1/360.0 - 128*k3/4275.0 - 2197*k4/75240.0 + k5/50.0 + 2*k6/55.0
        t += h}
    fmt.Printf("Ans: y(%v) = %v\n", target, y)
    fmt.Printf("Error: %v\n", err)
}
 
 
func main() {
    f := func(t, y float64) float64 {
        return y*y + t*t
    }
    t := 1.0
    y := 0.0
 
    // h = 0.1
    calcEuler(f, t, y, 0.1, 2)
    calcModifiedEuler(f, t, y, 0.1, 2)
    calcRungeKutta2(f, t, y, 0.1, 2)
    calcRungeKutta3(f, t, y, 0.1, 2)
    calcRungeKutta4(f, t, y, 0.1, 2)
    calcRungeKuttaFehlberg(f, t, y, 0.1, 2)
 
    // h = 0.05
    calcEuler(f, t, y, 0.05, 2)
    calcModifiedEuler(f, t, y, 0.05, 2)
    calcRungeKutta2(f, t, y, 0.05, 2)
    calcRungeKutta3(f, t, y, 0.05, 2)
    calcRungeKutta4(f, t, y, 0.05, 2)
    calcRungeKuttaFehlberg(f, t, y, 0.05, 2)
 
    // Validate
    calcRungeKuttaFehlberg(f, t, y, 0.01, 2)
}

---

< Last

Next >